The S-Propagator
formalism describes the dynamics in the structural organization
Fields and functional interactions
With the theoretical hierarchical framework
described in the section
theory,
I represent a physiological process, expressed by functional
interactions related to the geometry of the structure,
in terms of the transport of a field variable submitted
to the action of a field operator. Let 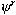 (r,t) be the field variable
defined in the r-space, e. g. membrane potential,
and let H be
the field operator which depends on
(r,t) be the field variable
defined in the r-space, e. g. membrane potential,
and let H be
the field operator which depends on 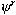 and on successive derivatives
and on successive derivatives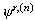 with respect to time
and space coordinates. The general form of the field equation
is given by :
with respect to time
and space coordinates. The general form of the field equation
is given by :
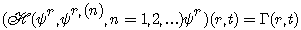 (3)
(3)
where Г is the source term. In this
equation, H
describes the propagation of the field variable
 from r’ to r, and
the local transformation in r is represented by
Г(r,t). Since the operator acts
from one point in space on another, it must take into
account the distance between these two points, and thus
include an interaction operator. More generally,
the influence of the location of the points, i.e. the
role of geometry on the dynamical processes, may be
studied by means of a field theory. The dynamical processes
that express the behavior of the related functional interactions
occur continuously in space and time with a finite velocity.
Thus, what is observed at point (r,t) results
from what was emitted at point (r’,t’), where
from r’ to r, and
the local transformation in r is represented by
Г(r,t). Since the operator acts
from one point in space on another, it must take into
account the distance between these two points, and thus
include an interaction operator. More generally,
the influence of the location of the points, i.e. the
role of geometry on the dynamical processes, may be
studied by means of a field theory. The dynamical processes
that express the behavior of the related functional interactions
occur continuously in space and time with a finite velocity.
Thus, what is observed at point (r,t) results
from what was emitted at point (r’,t’), where 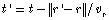 and vr is the velocity
of the interaction.
and vr is the velocity
of the interaction.
The finite value of the velocity
vr of the transport of the interaction,
i.e. the transport of molecules, potentials, currents,
or parametric effects depending on the elementary physiological
function, has a major effect on the behavior of the biological
system. This is particularly true of the delay
in the response between units. These effects are included
directly in the field interaction operator. Let us now
determine the specific operator that describes a physiological
mechanism.
S-Propagator dynamics
The units ui and u
are assumed to be at level r in the structural
organization (space scale k),
and at level T in the functional organization
(time scale T). The couple (k,T) in the 3-D representation
(Fig. 4) defines the organization of the
physiological function  .
.
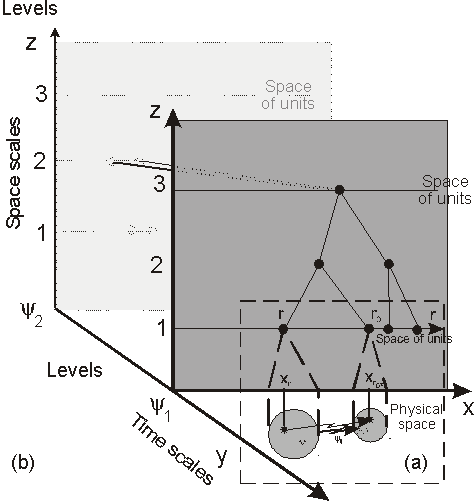
figure 4
There is a structural discontinuity between
the two units. Because of the hierarchy, ui
and u are associated with a non-local functional
interaction represented by the field  (r,t),
where r(x,y,z) is the coordinate in the
space of units refered to coordinates (x,y,z) in
the physical space. Using operators, the local time-variation
may be expressed as:
(r,t),
where r(x,y,z) is the coordinate in the
space of units refered to coordinates (x,y,z) in
the physical space. Using operators, the local time-variation
may be expressed as:
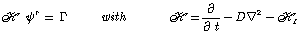 (4)
(4)
where HI is the non-local operator.
What are these operators? As shown in Figure 3,
in going from ui at r’ to u
at r, the functional interaction must cross the
structural discontinuity at the lower level, i.e. it must
use processes "outside" the level.
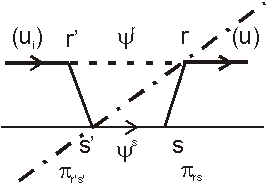
figure 3
In table A, the S-propagator
formalism has been summarized which leads from
Eq.(4) to the local time and non-local
space equation (A-8) for the dynamics of the field variable
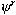 :
:
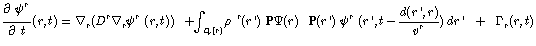
 (5)
(5)
(i)
(ii)
(iii)
where the sumation is on the domain Dr(r)
of the u-units connected with the units at r.
Here, Dr need not be constant, as the
medium may not be heterogeneous, in which case the term
may be space-dependent; the time scale is T, and
d(r’,r) is the distance between r’ and
r in the space of units u. The S-propagator
describes the functional action of u’ at r’
onto u at r per unit time, because
the field variable yr is emitted by
u’ at r’ and is transported to u
at r. Locally, the field variable depends on the
lower levels and is under three influences, which are
shown by the three terms in Eq.(5) : (i) a local process of diffusion
between units through the extra-unit space, i.e.
transport through the medium in which the units are located,
as defined by the diffusion constant Dr;
(ii) the S-propagator 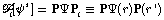 represents the transport of the field variable
through "homogeneous" structures at the lower level inside
ui or u, i.e. structures that
are homogeneous relative to the processes in a medium
with locally identical properties, without structural
discontinuities; and (iii) the generation of the field
variable at r as a result of local processes in
physical space, represented by the source term Гr, and possibly
due to the higher levels.
represents the transport of the field variable
through "homogeneous" structures at the lower level inside
ui or u, i.e. structures that
are homogeneous relative to the processes in a medium
with locally identical properties, without structural
discontinuities; and (iii) the generation of the field
variable at r as a result of local processes in
physical space, represented by the source term Гr, and possibly
due to the higher levels.
Finally, the determination of the dynamics
of physiological functions results from the determination
of the propagators P in the above Eq.(5). The linear case may be explicited.
In particular, this formalism is used for the dynamics
of the nervous system. These results are valid whatever
the level of organization. Because the same formalism
applies to each level of the hierarchy, it provides a
tool for the rigorous study of coupled biological systems
in terms of elementary mechanisms. As shown below, the
mechanisms included in Eq.5
provide the neural field equations.

