Hierarchical representation
for a biological theory of functional organization
(MTIP : Mathematical Theory of Integrative Physiology)
The conceptuel framework
The hierarchy and its consequences : Functional interactions
In the course of my work on physiological
models, ranging from the molecular to the organismal levels
(See Chauvet, "Theoretical systems
in Biology", page 143, Vol 1, Pergamon Press,
1996), some novel ideas specific to the study of biology
have been introduced, in particular the concepts of non-symmetric
and non-local functional interactions in hierarchical
space. These basic concepts emerged from a 'bottom-up'
approach to living systems, i.e. from a systematic study
of isolated physiological functions, followed by
the integration of these functions at the level
of the organism. A significant consequence of this theory
is that living organisms can be given not only a double
organizational representation, simultaneously structural
and functional, but also a double mathematical representation,
simultaneously geometrical and topological.
But what exactly is a physiological function?
We may compare it to a mathematical function in the sense
that the action of one structure on another results in
a certain product. The physiological function would then
be the action (the application, in mathematical
terms) and the product would be the result of the function
(the value of the function, in mathematical terms)
that is often identified with the physiological function
itself. Although this definition is general, it is unfortunately
not operational. It is relatively easy to describe particular
physiological functions such as vision, digestion, memorization
and so on, but it is far more difficult to give an operational
definition of a physiological function in general. One
possibility may be to define a physiological function
in terms of a combinatorial set of functional interactions
between structures. Such functional interactions are evidently
specific since they describe the action (whatever its
nature) of one structure on another or, more precisely,
the action of a source on a sink, after
the action has undergone a transformation in the source.
This action clearly possesses the property of non-symmetry.
In addition, it has another very important property, that
of non-locality, a notion somewhat more difficult
to appreciate since it stems from the structural hierarchy
of the system (see Chauvet, "Hierarchical functional
organization of formal biological systems", 1993),
i.e. certain structures are included in others. It may
be explained as follows. (i) From a mathematical point
of view, in a continuous representation, the action of
one structure on another is necessarily the action of
one point on another. This does not correspond to the
action of one cell on another in physical space since
a cell contains regions with specialized functions and
therefore cannot be reduced to a point. (ii) The interaction
between one structure and another has to operate across
other structures, which we have called structural discontinuities,
within which the processes follow a different course.
Thus, other levels of organisation in the hierarchical
system contribute to the working of a given structure
at a given level in the hierarchy. This is non-locality,
due to the choice of the representation, here the hierarchical
representation. Equations that represent processes have
then a different structure and must include non-local
terms.
The same reasoning applies to the dynamic
processes of functional interactions operating, for example,
between neural groups or between endocrine glands. In
more general terms, this can be extended to the entire
activity of the organism, provided that all the functional
interactions involved are correctly represented. We may
then formulate a hierarchical theory of functional organization
as follows: in a multiple-level hierarchical system,
each functional interaction is described by the transport
of an activating and/or inhibiting signal (in the form
of an action potential, a hormone or some other type of
interaction) between a source and a sink, and each physiological
function results from a combination of such interactions.
This idea can be conveniently expressed in terms of
a field theory according to which an operator transmits
an interaction at a certain rate from a source to a sink
situated in the space of units, with the source and the
sink each being reduced to a point. This representation
constitutes the basis for the definition of a physiological
function as the overall behavior of a group of structural
units within a hierarchical system.
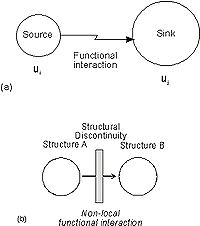
figure 1
From the mathematical point of view :
(i) A functional interaction is defined
as the interaction between two of the p structural units
ui and uj (i,j
= 1,p) of a formal biological system (FBS). One
of the units, for example ui, emits a
signal that acts on the other, uj, which
in turn emits a substance, after an eventual transformation
f :
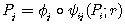(1)
This interaction, called an elementary
function, is represented by yij (Figure
1) and constitutes an element of the mathematical
graph representing the organization of the formal
biological system (O-FBS). The dynamics of the functional
interactions is then described by a system of equations
of the type:
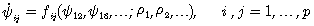(2)
where the r 's are specific physical
or geometrical parameters.
(ii) The structural unit is defined
as the set of anatomical or physical elements intervening
in the physiological function.
Thus, from a functional point of view, a
system made up of a set of elements, such as molecules,
cellular organelles, cells, tissues and organs, is represented
by functional interactions and structural units.
This structural hierarchy is shown in Figure 2.
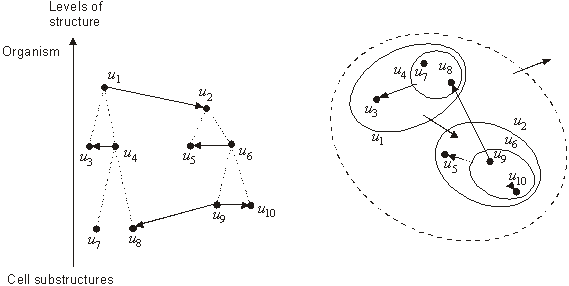figure 2
Functional interactions
are identified by structural discontinuities
Functional interactions may be identified by the presence
of structural discontinuities. Suppose we have two
structural units separated by a structural discontinuity.
The interaction is propagated from one unit to the other
across the discontinuity, which could for example be a membrane
allowing active transport. The membrane is at a lower level
in the structural hierarchy compared to the two interacting
units. From the point of view of the dynamics of the functional
interaction, we may say that this interaction consists of
a certain physiological process operating in the two units
(located at r’ and r in the space of units,
i.e. the r-space, refered to r’(x’,y’,z’)
and r(x,y,z) in the physical three-dimensional
space), with a different physiological process being executed
at a lower level in the structural discontinuity. A functional
interaction may be represented in the form of a diagram
as shown in Figure 3. The equation governing
the transport of the interaction applies to a continuous
medium and explains why the equation of the process is different
at the lower level of organization. This observation constitutes
the basis of a new formalism (see Chauvet, 1999, 2002) involving
what we have called structural propagators (S-propagators).
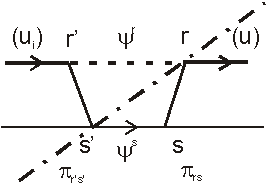
figure 3
A three-dimensional
representation of a biological system
As we have seen, a physiological function
may be represented by a mathematical graph in which the
nodes correspond to the structural units and the edges correspond
to the oriented, non-symmetric interactions. All physiological
functions are intricately linked in a hierarchical fashion.
They are linked relatively to space, which is evident, but
also to time, which represents a different evolution rate
with physiological fonctions.. Probably the best way to
realize this aspect of the hierarchy is to consider the
intricated time loops of the algorithm that represents the
working of the function. We have therefore to consider not
only the structural hierarchy but also the functional
hierarchy of the system. Then, each level of the functional
organization will correspond to a particular physiological
function, i.e. a process that occurs on a certain time scale.
How do we define these two types of hierarchy? It is convenient
to consider the structural hierarchy as being organized
along the space scales of a physiological process
while the functional hierarchy is organized according to
the corresponding time scales. Moreover, it offers
the advantage of clearly separating the structural and functional
organizations, i.e. the structure and the function of the
biological system studied.
This “separation” may be viewed as follows.
Using axes for the space scales, the time scales and the
space of structural units, we have a three-dimensional representation
of a physiological function (Figure 4), showing:
The structural units in space for a given
function; and the hierarchical organization of physiological
functions for a given space scale.
The integration of physiological functions,
i.e. the identification of the couplings between the functions,
requires determination of the functional interactions at
the different hierarchical levels involved.
For example, the interactions at the molecular
level between angiotensin and renin will be situated at
the lowest level of the hierarchical organization representing
blood circulation, and will themselves be coupled with the
neural network. This complex task can only be undertaken
using the highly abstract and technically advanced
mathematical methods.
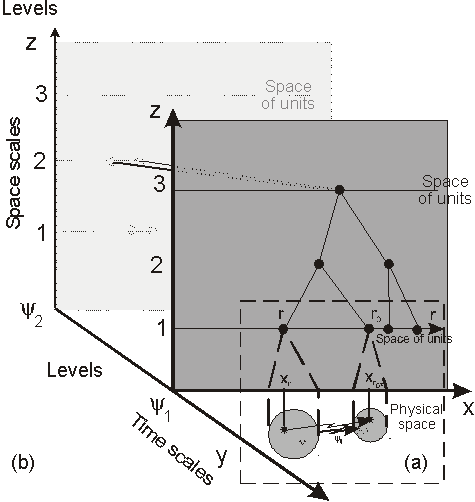
figure 4
