Représentation
hiérarchique pour une théorie biologique
de l'organisation fonctionnelle (MTIP :
Mathematical Theory of Integrative
Physiology)
La hiérarchie et ses conséquences :
l'interaction fonctionnelle
Au cours de mon travail sur
les modèles physiologiques, du niveau
moléculaire au niveau de l'organisme (voir
Chauvet "Theoretical
systems in Biology", page 143, Vol 1,
Pergamon Press, 1996), j'ai introduit de
nouvelles idées spécifiques à l'étude de la
biologie, en particulier le concept
d'interaction fonctionnelle non symétrique
et non locale dans un espace
hiérarchique. Ces concepts fondamentaux ont
émergé d'une approche bottom-up des systèmes
vivanst, autrement dit d'une étude
systématique des fonctions physiologiques
isolées, suivie par l'intégration de ces
fonctions au niveau de l'organisme. Une
conséquence significative de cette théorie est
que les organismes vivants ne sont pas
seulement vus comme une double représentation
organisationnelle, simultanément structurale
et fonctionnelle, mais aussi vus sous la forme
d'une double représentation mathématique, à la
fois géométrique et topologique.
Mais qu'est-ce exactement
qu'une fonction physiologique ? Nous pouvons
la comparer à une fonction mathématique dans
le sens où l'action d'une structure sur une
autre entraîne un certain produit. La fonction
physiologique serait alors l'action (l'application
en termes mathématiques) et le produit serait
le résultat de la fonction (la valeur
de la fonction en termes mathématiques) qui
est souvent identifiée à la fonction
physiologique elle-même. Bien que cette
définition soit générale, elle est
malheureusement inopérante. Il est
relativement facile de décrire les fonctions
physiologiques particulières comme la vision,
la digestion, la mémorisation, etc. mais il
est beaucoup plus difficile de donner une
définition opérationnelle d'une fonction
physiologique en général. Une possibilité est
de définir une fonction physiologique comme
une combinaison d'interactions fonctionnelles
entre structures. De telles interactions
fonctionnelles sont évidemment spécifiques
puisqu'elles décrivent l'action (quelle que
soit sa nature) d'une structure sur une autre
ou, plus précisément, l'action d'une source
sur un puits après que l'action ait subi une
transformation dans la source
(c'est-à-dire ait entraîné une transformation
dans le puits). Il est donc clair que l'
interaction possède la propriété de non
symétrie source vers puits . En outre,
elle montre une autre propriété très
importante : celle de non localité,
définition un peu plus difficile à comprendre
puisqu'elle prend son origine dans la
hiérarchie structurale du système (voir
Chauvet, "Hierarchical functional organization
of formal biological systems", 1993)),
c'est-à-dire que certaines structures sont
incluses dans d'autres. La non localité peut
être expliquée comme suit :
Le même raisonnement
s'applique aux processus dynamiques des
interactions fonctionnelles, opérant par
exemple sur groupes de neurones ou glandes
endocrines. En termes plus généraux, il peut
être étendu à l'activité complète de
l'organisme, pourvu que toutes les
interactions fonctionnelles impliquées soient
correctement représentées. Nous pouvons alors
formuler une théorie hiérarchique de
l'organisation fonctionnelle de la façon
suivante :
dans un système hiérarchique à n niveaux,
chaque interaction fonctionnelle est décrite
par le transport d'un signal activateur et/ou
inhibiteur (sous la forme d'un potentiel
d'action d'une hormone ou de tout autre type
d'interaction) entre une source et un puits,
et chaque fonction physiologique est la
conséquence d'une combinaison de telles
interactions. Cette idée peut être commodément
exprimée par une théorie du champ selon
laquelle un opérateur transmet une interaction
à une vitesse donnée d'une source vers un
puits situé dans l'espace des unités, la
source et le puits étant chacun réduit à un
point. Cette représentation constitue la base
de la définition d'une fonction physiologique
comme le comportement global d'un groupe
d'unités structurales dans un système
hiérarchique.
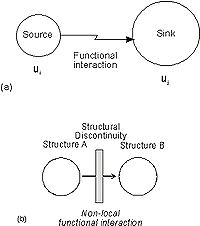
figure 1
Du point de vue mathématique :
(i) une interaction
fonctionnelle est définie comme
l'interaction entre deux des p unités
structurales ui et uj (i,j =
1,p) d'un système biologique formel
(FBS). L'une des unités, par exemple ui,
emet un signal qui agit sur l'autre unité, uj,
qui en retour emet une subtance, après une
éventuelle transformation f :
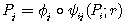 (1)
(1)
Cette interaction, appelée fonction
élémentaire, est représentée par by yij
(Figure 1) et constitue un
élément du graphe mathématique qui représente
l'organisation du système biologique formel
(O-FBS). La dynamique des interactions
fonctionnelles est alors décrite par un
système d'équations du type suivant :
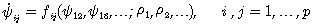 (2)
(2)
ou r 's sont des
paramètres physiques ou géométriques
spécifiques.
(ii) L'unité structurale est
définie comme l'ensemble des éléments
anatomiques ou physiques intervenant dans la
fonction physiologique.
Donc d'un point de vue
fonctionnel, un système constitué d'un ensemble
d'éléments comme des molécules, des organites
cellulaires, des cellules, des tissus et des
organes est représenté par des interactions
fonctionnelles entre unités structurales. Cette
hiérarchie structurale est montrée Figure
2.
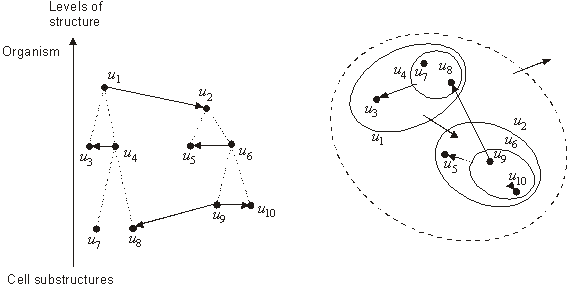 figure 2
figure 2
Les interactions
fonctionnelles sont identifiées par des
discontinuités structurales
Les interactions fonctionnelles peuvent être
identifiées par la présence de discontinuités
structurales. Supposons que nous ayons
deux unités structurales séparées par une
discontinuité structurale. L'interaction se
propage d'une unité à l'autre à travers cette
discontinuité qui pourrait être par exemple une
membrane, siège d'un transport actif. La
membrane est au niveau inférieur dans la
hiérarchie structurale, par rapport aux deux
unités en interaction. Du point de vue de la
dynamique de l'interaction fonctionnelle, on
peut dire qu'elle consiste en un certain
processus physiologique opérant dans les deux
unités (localisées en r' et r
dans l'espace des unités, c'est-à-dire le r-espace
qui se réfère à r'(x,' y', z') et r(x,y,z)
dans l'espace physique tridimensionnel, avec un
processus physiologique différent ayant lieu au
niveau inférieur dans la discontinuité
structurale. Une interaction fonctionnelle peut
être représentée sous la forme d'un diagramme,
comme le montre la figure 3.
L'équation gouvernant le transport de
l'interaction s'applique à un milieu continu et
explique pourquoi l'équation du processus est
différente au niveau inférieur de
l'organisation. Cette observation constitue la
base d'un nouveau formalisme (voir Chauvet,
1999, 2002) impliquant ce que j'ai appelé les S
propagateurs (propagateurs dans les structures).
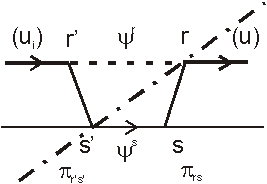
figure 3
Une représentation
tridimensionnelle d'un système biologique
Comme on l'a vu, une fonction
physiologique peut être représentée par des
graphes mathématiques où les nœuds correspondent
aux unités structurales et les arêtes aux
interactions orientées, non-symétriques. Toutes
les fonctions physiologiques sont couplées de
façon intriquée dans la hiérarchie. Elles sont
liées relativement à l'espace - ce qui est
évident - mais aussi au temps qui correspond à
une vitesse d'évolution différente des fonctions
physiologiques (échelle de temps différente).
Probablement la meilleure façon de voir cet
aspect de la hiérarchie est de considérer les
boucles intriquées en temps de l'algorithme qui
représente l'évolution de la fonction. Nous
devons donc non seulement considérer la
hiérarchie structurale mais aussi la hiérarchie
fonctionnelle du système. Alors, chaque
niveau de l'organisation fonctionnelle
correspondra à une fonction physiologique
particulière, c'est-à-dire à un processus qui se
réalise dans une certaine échelle de temps.
Comment définir ces deux types de hiérarchies ?
Il est commode de considérer la hiérarchie
structurale comme étant organisée selon les
échelles d'espace d'un processus physiologique,
alors que la hiérarchie fonctionnelle est
organisée selon les échelles de temps. De plus,
ceci offre l'avantage de séparer clairement les
organisations structurales et fonctionnelles,
c'est-à-dire la structure et la fonction du
système biologique étudié.
Cette “séparation” peut être
représentée en utilisant des axes pour les
échelles d'espace, les échelles de temps, et
l'espace des unités structurales. Nous obtenons
une représentation tridimensionnelle d'une
fonction physiologique (Figure 4)
qui montre :
- les unités structurales dans
l'espace pour une fonction donnée et
l'organisation hiérarchique des fonctions
physiologiques pour une échelle d'espace donnée.
- l'intégration des fonctions
physiologiques, c'est-à-dire l'identification
des couplages entre les fonctions, qui requiert
de déterminer les interactions fonctionnelles
aux différents niveaux hiérarchiques impliqués
Par exemple, les interactions
au niveau moléculaire entre l'angiotensine et la
rénine seront situées au niveau le plus bas de
l'organisation hiérarchique représentant la
circulation du sang, et seront elle-même
couplées au réseau neuronal. Ce travail complexe
peut seulement être entrepris en utilisant des méthodes
mathématiques hautement abstraites et
techniquement avancées:, ce
que j'ai appelé la MTIP (Mathematical Theory of
Integrative Physiology).
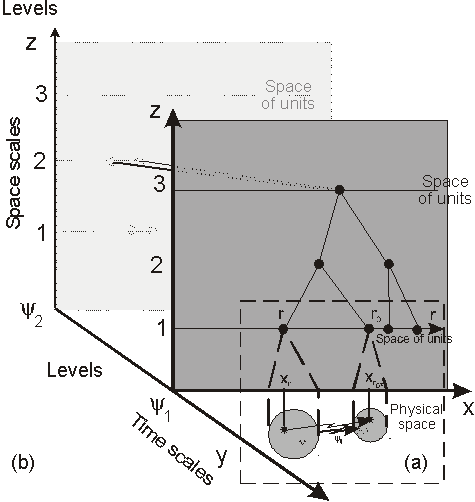
figure 4

